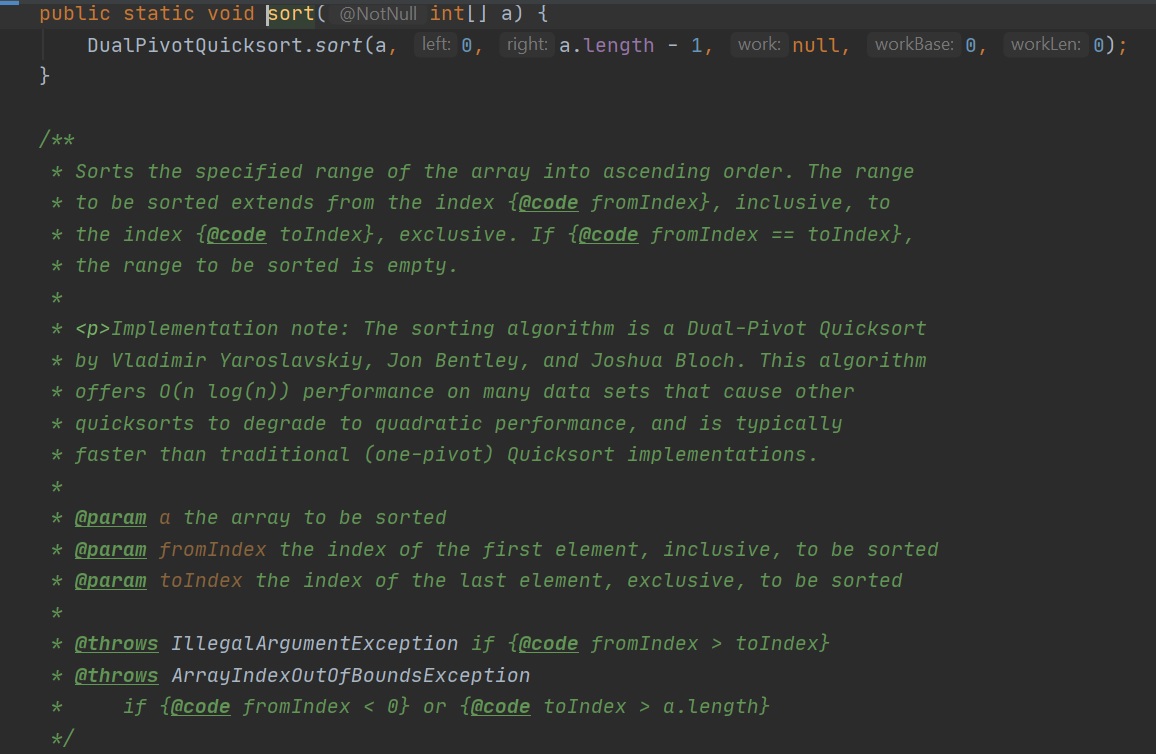
I am briefly going to cover a number of well known sorting algorithms, use the Big-O cheatsheet for the Big-O notation for each regarding time complexity.
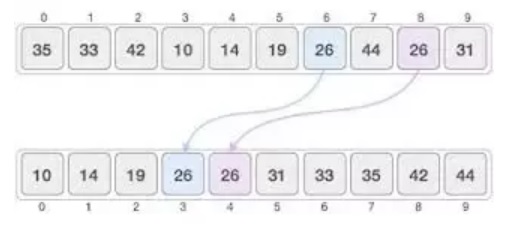
One area to cover before we start is the different between stable and unstable sorting, this is where if two numbers are the same value, you may not be woprried if using numbers but it may be if you are using Objects.
- stable - original ordering will be preserved (see diagram below element 6 comes before element 8)
- unstable - original ordering will not be preserved
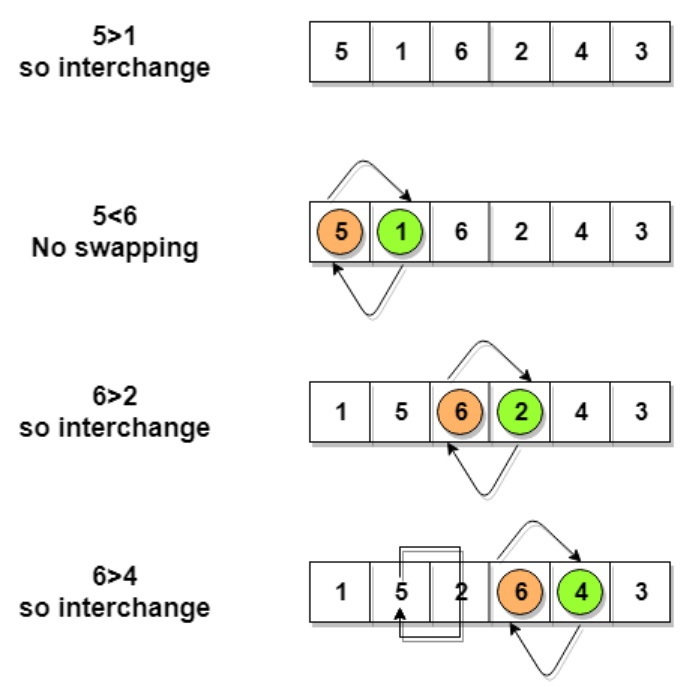
Bubble sort algorithm performance degrades the more elements, first index 0 is compared with index 1, if its greater we swap the elements, if not the elements stay the same, then we move onto index 1 and compare index 1 with index 2 and swap if greater or move to index 2 if not, this repeats until thend, what this is actually doing is moving the greatest number to the end (right-side ) of the array, once at the end we repeat the whole process but exclude the last element as it has already been sorted. You can see an example of this below, on the first pass 6 will be positioned at the end of the array on the second pass 5 will be in position 4 (index starting at 0), etc. The more elements the more passes we have to perform and thus decreases the performance. With bubble sort you can sort in both directions right-side of the array either the lowest of highest value.
- In-place algorithm
- O(n2) time complexity (two loops in the code)
- it will take 100 steps to sort 10 items, 10,000 steps = 100 items, 1,000,000 steps = 1,000 items
- it degrades the more items that you have
- stable sorting - only swap if elements if are greater (or less), we don't swap if equal
| Bubble Sort (there are many different versions) | package uk.co.datadisk.sorting;
public class Main_Bubble_Sort {
// Degrades the more elements you have
public static void main(String[] args) {
int[] bubbleArray = {20, 35, -15, 7, 55, 1, -22};
int unsortedPartitionIndex = bubbleArray.length - 1;
// Sort the array
while(unsortedPartitionIndex != 0) {
for(int i = 0; i < unsortedPartitionIndex; i++){
if(bubbleArray[i] > bubbleArray[i+1]){
swap(bubbleArray, i, i +1);
}
}
unsortedPartitionIndex--;
}
// Print the array
for(int i = 0; i < bubbleArray.length; i++){
System.out.println(bubbleArray[i]);
}
}
public static void swap(int[] array, int i, int j) {
int tmp;
tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
} |
Selection Sort goes through the array looking for the highest value and making a note of its position, once the highest value has been found it will then swap the last index position (index 6) with the highest position (index 4), it will then repeat but swap the highest position with highest index position - 1 (index 5)
- In-place algorithm
- O(n2) time complexity (two loops in the code)
- it will take 100 steps to sort 10 items, 10,000 steps = 100 items, 1,000,000 steps = 1,000 items
- does not require much swapping as bubble sort
- unstable sorting, could swap even if its a duplicate number
First pass highest index will be 4
We swap index 4 with index 6
next iteration we swap index 1 with index 5, continue until array is sorted| Selection Sort | package uk.co.datadisk.sorting;
public class Main_Selection_Sort {
// Uses less swaps than selection sort
public static void main(String[] args) {
int[] selectionArray = {20, 35, -15, 7, 55, 1, -22};
for ( int lastUnsortedIndex = selectionArray.length - 1; lastUnsortedIndex > 0; lastUnsortedIndex--){
int largest_element = 0;
for( int i = 1; i <= lastUnsortedIndex; i++){
if(selectionArray[i] > selectionArray[largest_element]) {
largest_element = i;
}
}
swap(selectionArray,largest_element, lastUnsortedIndex);
}
for(int i = 0; i < selectionArray.length -1; i++){
System.out.println(selectionArray[i]);
}
}
public static void swap(int[] array, int i, int j) {
int tmp;
tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
} |
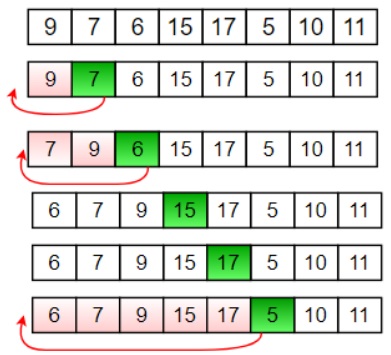
Insertion Sort index 0 will hold the lowest value, we start by working our way through the array shifting elements down (index 0) until they are in position, so first pass 9 gets shifted down to index 1 so that 7 can go into index 6, second pass 7 and 9 get shifted down so that 6 can go into index 0, this continues until the array is sorted, note that elements are shift down to make room if a element is of a lower value.
- In-place algorithm
- O(n2) time complexity (two loops in the code)
- it will take 100 steps to sort 10 items, 10,000 steps = 100 items, 1,000,000 steps = 1,000 items
- does not require much swapping as bubble sort
- stable sorting
| Insertion Sort | package uk.co.datadisk.sorting;
public class Main_Insertion_Sort {
public static void main(String[] args) {
int[] insertionArray = {20, 35, -15, 7, 55, 1, -22};
for(int firstUnsortedIndex = 1; firstUnsortedIndex < insertionArray.length; firstUnsortedIndex++){
int newElement = insertionArray[firstUnsortedIndex];
int i;
for(i = firstUnsortedIndex; i > 0 && insertionArray[i - 1] > newElement; i--){
insertionArray[i] = insertionArray[i - 1];
}
insertionArray[i] = newElement;
}
for(int i = 0; i < insertionArray.length -1; i++){
System.out.println(insertionArray[i]);
}
}
} |
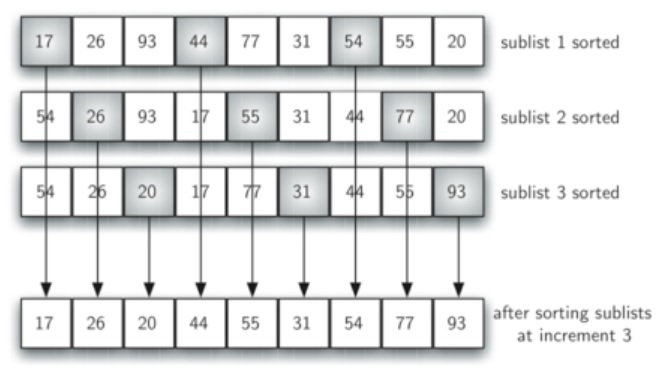
Shell Sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left. Depending on the gap value the time complexity changes, you can select a formula that determines the gap value for you toi get the best out of the algorithm. The example below shows a gap of 3
- In-place algorithm
- depending of the gap but worst is O(n2) time complexity but can be much better
- does not require much shifting as insertion sorting
- unstable sorting
| Shell Sort | package uk.co.datadisk.sorting;
public class Main_Shell_Sort {
public static void main(String[] args) {
int[] shellArray = {20, 35, -15, 7, 55, 1, -22};
// reduce the gap for each iteration, but start with length / 2 ( gap = 3 to start)
for(int gap = shellArray.length / 2; gap > 0; gap /= 2){
// this is insertion sort but using gap
for (int i = gap; i < shellArray.length; i++){
int newElement = shellArray[i];
int j = i;
while(j >= gap && shellArray[j - gap] > newElement){
System.out.println("GAP " + gap + ": " + newElement + " " + shellArray[j - gap]);
shellArray[j] = shellArray[j - gap];
j -= gap;
}
shellArray[j] = newElement;
}
}
for(int i = 0; i < shellArray.length -1; i++){
System.out.println(shellArray[i]);
}
}
}
output
------------------------------
GAP 3: 7 20
GAP 3: -22 20
GAP 3: -22 7
GAP 1: -15 35
GAP 1: 7 35
GAP 1: 1 55
GAP 1: 1 35
GAP 1: 1 7
GAP 1: 20 55
GAP 1: 20 35 |
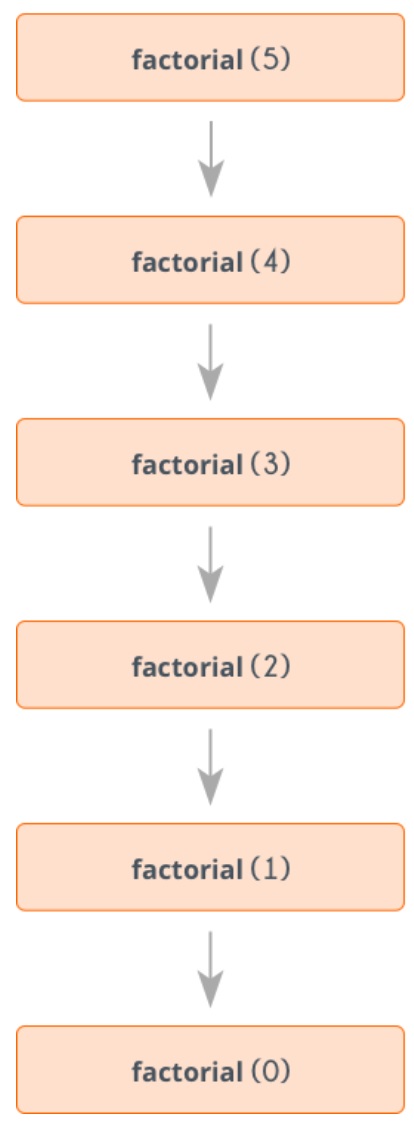
Recursion is a method that recalls itself, it has a termination condition so that successive repetitions are processed up to the critical step where the condition is met at which time the rest of each repetition is processed from the last one called to the first.
| Recursion | package uk.co.datadisk.sorting;
public class Main_Recursion {
public static void main(String[] args) {
System.out.println(iterativeFactorial(3));
System.out.println("------------------------------");
System.out.println(recursiveFactorial(3));
}
public static int iterativeFactorial(int num){
if (num == 0 ){
return 1;
}
int factorial = 1;
for(int i = 1; i <= num; i++){
factorial *= i;
}
return factorial;
}
public static int recursiveFactorial(int num){
if (num == 0 ){ // breaking condition (base case) MUST HAVE
System.out.println("Base case " + (num - 1));
return 1;
}
System.out.println("Calling recursiveFactorial " + (num - 1));
// n! = n *(n - 1)!
return num * recursiveFactorial(num - 1);
}
} |
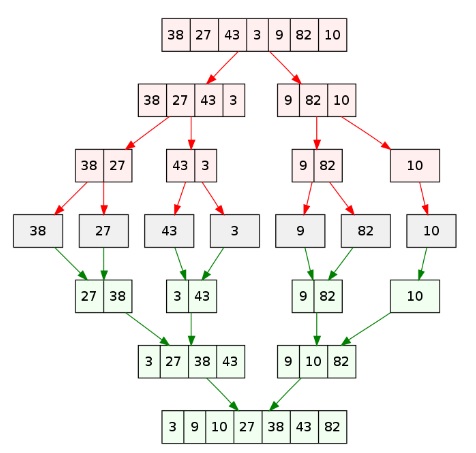
Merge sort is a divide and conquer algorithm, basically the array gets split, and then sorted and then merged. We don't create any new arrays but peform a logical split. Merge sort uses recursion (see above) to split the array and perform the sorting/merging.
- NOT an In-place algorithm
- O(nlogn) base 2, we keeping dividing the array in half
- stable sorting
| Merge Sort (uncomment debugging statements to drill down on what is happening) | package uk.co.datadisk.sorting;
public class Main_Merge_Sort {
public static void main(String[] args) {
int[] mergeArray = {20, 35, -15, 7, 55, 1, -22};
mergeSort(mergeArray, 0, mergeArray.length);
displayArray(mergeArray, "mergeArray (complete)");
}
public static void mergeSort(int[] input, int start, int end){
if( end - start < 2){
return;
}
// get the middle of the array
int mid = (start + end) / 2;
//System.out.println("MergeSort mid: " + mid);
// left side of array
//System.out.println("mergeSort calling left side start: " + start + " mid: " + mid);
mergeSort(input, start, mid);
// right side of the array
//System.out.println("mergeSort calling right side mid: " + mid + " end: " + end);
mergeSort(input, mid, end);
// Just merge the left and right hand sides
displayArray(input, "mergeArray (not complete)");
merge(input, start, mid, end);
}
public static void merge(int[] input, int start, int mid, int end){
//System.out.println("merge called........ start: " + start + " mid: " + mid + " end: " + end);
if(input[mid - 1] <= input[mid]){
return;
}
int i = start;
int j = mid;
int tempIndex = 0;
//System.out.println("merge i: " + i + " j: " + j + " tempIndex: " + tempIndex);
int[] temp = new int[end - start];
while(i < mid && j < end){
// <= makes it a stable array to handle duplicates
temp[tempIndex++] = input[i] <= input[j] ? input[i++] : input[j++];
//displayArray(temp, "temp");
}
// src, srcPosition, dest, destPosition, length
//System.out.println("merge - input copy i: " + i + " destPos: " + (start + tempIndex) + " length: " + (mid - 1));
System.arraycopy(input, i, input, start + tempIndex, mid - i);
//displayArray(input, "input");
//System.out.println("merge - temp copy start: " + start + " tempIndex: " + tempIndex);
System.arraycopy(temp, 0, input, start, tempIndex);
//displayArray(input, "input");
}
public static void displayArray(int[] input, String name){
System.out.print("Array " + name + ": ");
for(int i = 0; i < input.length; i++){
System.out.print(input[i] + " ");
}
System.out.println();
}
}
Output
----------------------------------
Array mergeArray (not complete): 20 35 -15 7 55 1 -22
Array mergeArray (not complete): 20 -15 35 7 55 1 -22
Array mergeArray (not complete): -15 20 35 7 55 1 -22
Array mergeArray (not complete): -15 20 35 7 55 1 -22
Array mergeArray (not complete): -15 20 35 7 55 -22 1
Array mergeArray (not complete): -15 20 35 -22 1 7 55
Array mergeArray (complete): -22 -15 1 7 20 35 55 |
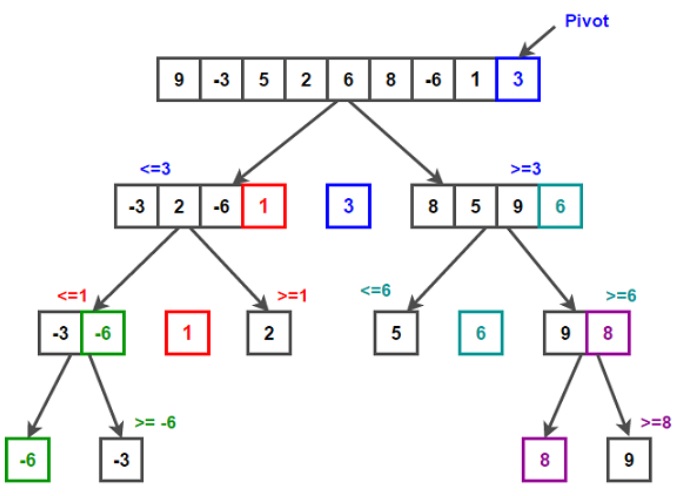
Quick Sort is another algorithm that uses divide and conquer, a pivot element is choosen to partition the array into two parts, elements less than the pivot go into the left-side array and elements that are greater go into the right-side array and thus the pivot will be in its correct position, then we repeat the process for each of the two parts. The pivot can be at the front or end of the array.
- In-place algorithm
- O(nlogn) base 2, we keeping dividing the array in half using a pivot
- will in most cases be better than merge sort
- unstable sorting
In the below example pivots numbers will be 3 then 1 then 6 then -6 and finally 8.
| Quick Sort (using first element of array as pivot) | package uk.co.datadisk.sorting;
public class Main_Quick_Sort {
public static void main(String[] args) {
int[] quickArray = {20, 35, -15, 7, 55, 1, -22};
displayArray(quickArray, "quickArray - Start");
quickSort(quickArray, 0, quickArray.length);
displayArray(quickArray, "quickArray - End");
}
public static void quickSort(int[] input, int start, int end) {
if (end - start < 2) {
return;
}
int pivotIndex = partition(input, start, end);
quickSort(input, start, pivotIndex);
quickSort(input, pivotIndex + 1, end);
}
private static int partition(int[] input, int start, int end) {
// This is using the first element as the pivot
int pivot = input[start];
int i = start;
int j = end;
while (i < j) {
// Empty loop body
// looking from right to left (smaller elements)
while (i < j && input[--j] >= pivot);
if (i < j) {
//System.out.println("Replacing " + input[i] + " with " + input[j]);
input[i] = input[j];
//displayArray(input, "input");
}
// looking from left to right (larger elements)
while (i < j && input[++i] <= pivot);
if (i < j) {
//System.out.println("Replacing " + input[j] + " with " + input[i]);
input[j] = input[i];
//displayArray(input, "input");
}
}
input[j] = pivot;
//displayArray(input, "input");
return j;
}
public static void displayArray(int[] input, String name) {
System.out.print("Array " + name + " - ");
for (int i = 0; i < input.length; i++) {
System.out.print(input[i] + " ");
}
System.out.println();
}
} |
Counting Sort makes assumptions about the data, its based on keys between a specific range (not too large). It works by counting the number of objects having distinct key values (kind of hashing). Then doing some arithmetic to calculate the position of each object in the output sequence. Counting sort only works with non-negative discrete values (no floats, strings, etc), normally used with whole numbers. A counting array is created to count each number found.
- NOT an In-place algorithm
- O(n) this is because we are making assumptions about the data
- will in most cases be better than merge sort
- stable sorting but extra steps are required
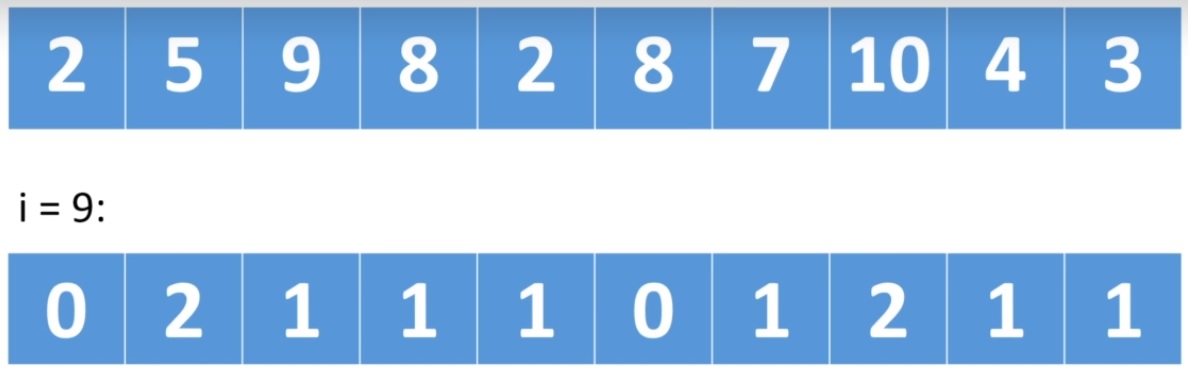we count each value and increase the number in the counting array
we then use the counting array to rewrite the array but in order| Counting Sort | package uk.co.datadisk.sorting;
public class Main_Counting_Sort {
public static void main(String[] args) {
int[] intArray = {2, 5, 9, 8, 2, 8, 7, 10, 4, 3};
countingSort(intArray, 1, 10);
displayArray(intArray, "countArray");
}
public static void countingSort(int[] input, int min, int max){
int[] countArray = new int[(max - min) + 1];
for(int i = 0; i < input.length; i++){
countArray[input[i] - min]++;
}
int j = 0;
for(int i = min; i <= max; i++){
while(countArray[i - min] > 0){
input[j++] = i;
countArray[i - min]--;
}
}
}
public static void displayArray(int[] input, String name) {
System.out.print("Array " + name + " - ");
for (int i = 0; i < input.length; i++) {
System.out.print(input[i] + " ");
}
System.out.println();
}
} |
Radix Sort is an integer sorting algorithm that sorts data with integer keys by grouping the keys by individual digits that share the same significant position and value (place value). Radix sort uses counting sort as a subroutine to sort an array of numbers. The data must have the same radix (radix for decimal is 10, alphabet is 26, binary numbers is 2, etc) and width (number of digits or letters so "hello" is 5, 1000 is 4, etc), so beause of this data must be integers or strings.
- In-place algorithm depending on the sort alogrithm used
- O(n) this is because we are making assumptions about the data
- slower than O(nlogn) because of the overhead involved
- stable sorting
we sort by the 1's position
we sort by the 10's position
finally we sort by the 1000's position| Radix Sort | package uk.co.datadisk.sorting;
public class Main_Radix_Sort {
public static void main(String[] args) {
int[] radixArray = { 4725, 4586, 1330, 8792, 1594, 5729 };
radixSort(radixArray, 10, 4); // base 10
displayArray(radixArray, "Radix Array");
}
public static void radixSort(int[] input, int radix, int width) {
for (int i = 0; i < width; i++) {
radixSingleSort(input, i, radix);
}
}
public static void radixSingleSort(int[] input, int position, int radix) {
int numItems = input.length;
int[] countArray = new int[radix];
for (int value: input) {
countArray[getDigit(position, value, radix)]++;
}
// Adjust the count array
for (int j = 1; j < radix; j++) {
countArray[j] += countArray[j - 1];
}
int[] temp = new int[numItems];
for (int tempIndex = numItems - 1; tempIndex >= 0; tempIndex--) {
temp[--countArray[getDigit(position, input[tempIndex], radix)]] =
input[tempIndex];
}
for (int tempIndex = 0; tempIndex < numItems; tempIndex++) {
input[tempIndex] = temp[tempIndex];
}
}
public static int getDigit(int position, int value, int radix) {
return value / (int) Math.pow(radix, position) % radix;
}
public static void displayArray(int[] input, String name) {
System.out.print("Array " + name + " - ");
for (int i = 0; i < input.length; i++) {
System.out.print(input[i] + " ");
}
System.out.println();
}
} |
The Java JDK has some builtin sort algorithms, for sorting or parrallel sorting
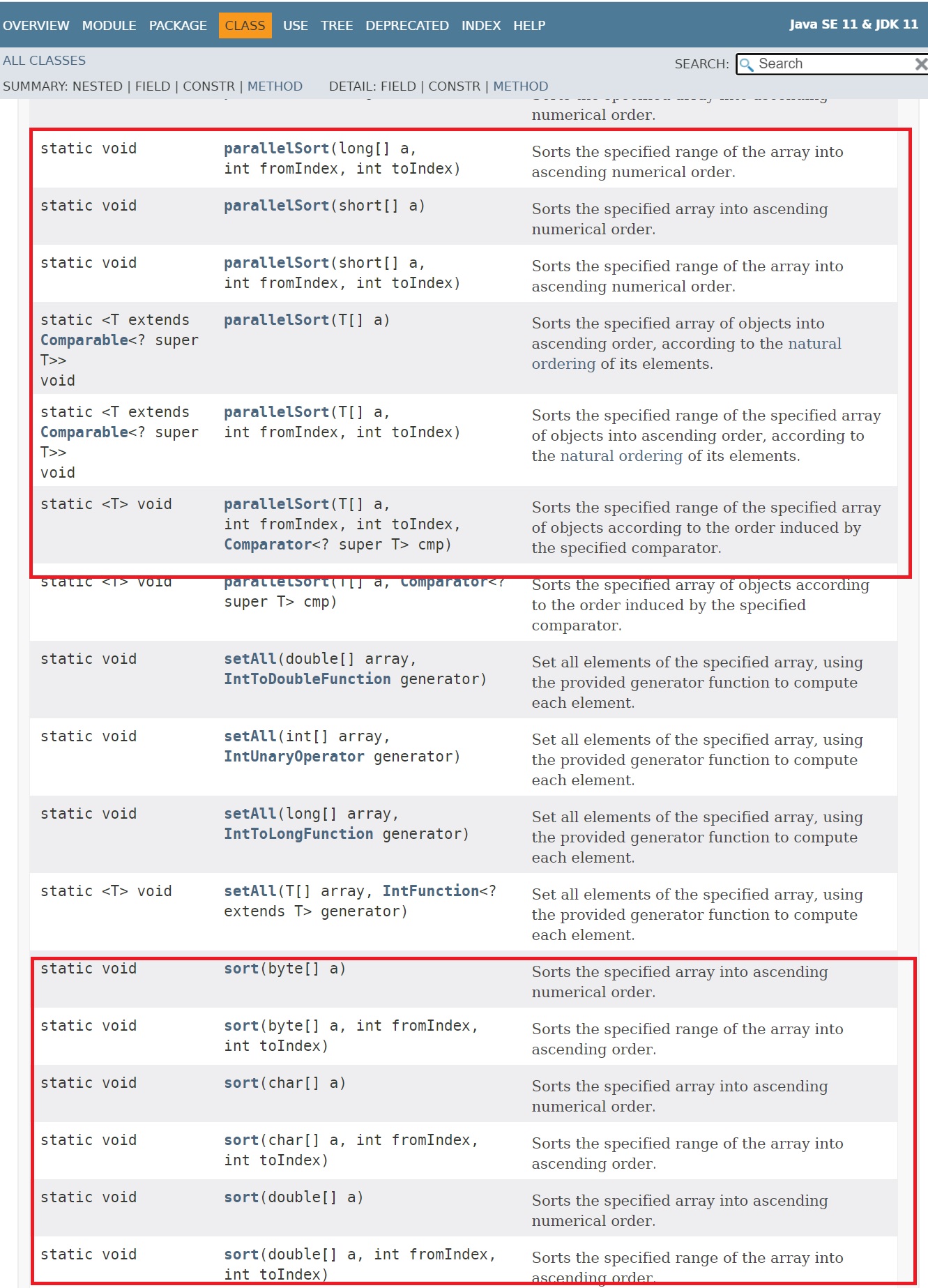
| Sorting and ParallelSorting using JDK | package uk.co.datadisk.sorting;
import java.util.Arrays;
public class Main_JDK_Sort {
public static void main(String[] args) {
int[] jdkArray = {20, 35, -15, 7, 55, 1, -22};
int[] jdkParallelArray = {20, 35, -15, 7, 55, 1, -22};
Arrays.sort(jdkArray);
displayArray(jdkArray, "jdkArray");
Arrays.parallelSort(jdkParallelArray);
displayArray(jdkParallelArray, "jdkParallelArray");
}
public static void displayArray(int[] input, String name){
System.out.print("Array " + name + ": ");
for(int i = 0; i < input.length; i++){
System.out.print(input[i] + " ");
}
System.out.println();
}
} |
Using your IDE, you can see what kinda of sorting algorithm is being used, in Intellij use go to -> declaration
